Basic Statistical Tests

Outline

  • p-values

  • confidence intervals

  • t-tests

  • chi-square tests

  • simple regression

Five Step Hypothesis Testing Procedure

  • Step 1: State your null and alternate hypothesis.

  • Step 2: Collect data.

  • Step 3: Perform a statistical test.

  • Step 4: Decide whether to reject or fail to reject your null hypothesis.

  • Step 5: Present your findings.

Statistical Hypotheses

  • Null Hypothesis what we are hoping to disprove?

  • Alternative Hypothesis if random chance isn’t the reason, then what?

What is a p-value?

Image source: Susan VanderPlas UNL Extension

What is a p-value?

Image source: Susan VanderPlas UNL Extension

What is a confidence interval?

Confidence intervals are a range of values around the central estimate obtained from the sample data.

Image source: Susan VanderPlas UNL Extension

Penguins Data

data(penguins, package = "palmerpenguins")

Two-sample independent t-test

Research Question Is there a difference in the body mass (g) of penguins between male and female penguins?

Data

sex body_mass_g
male 3750
female 3800
female 3250

Numerical Summary

sex mean sd
female 3862.3 666.2
male 4545.7 787.6

Graphical Summary

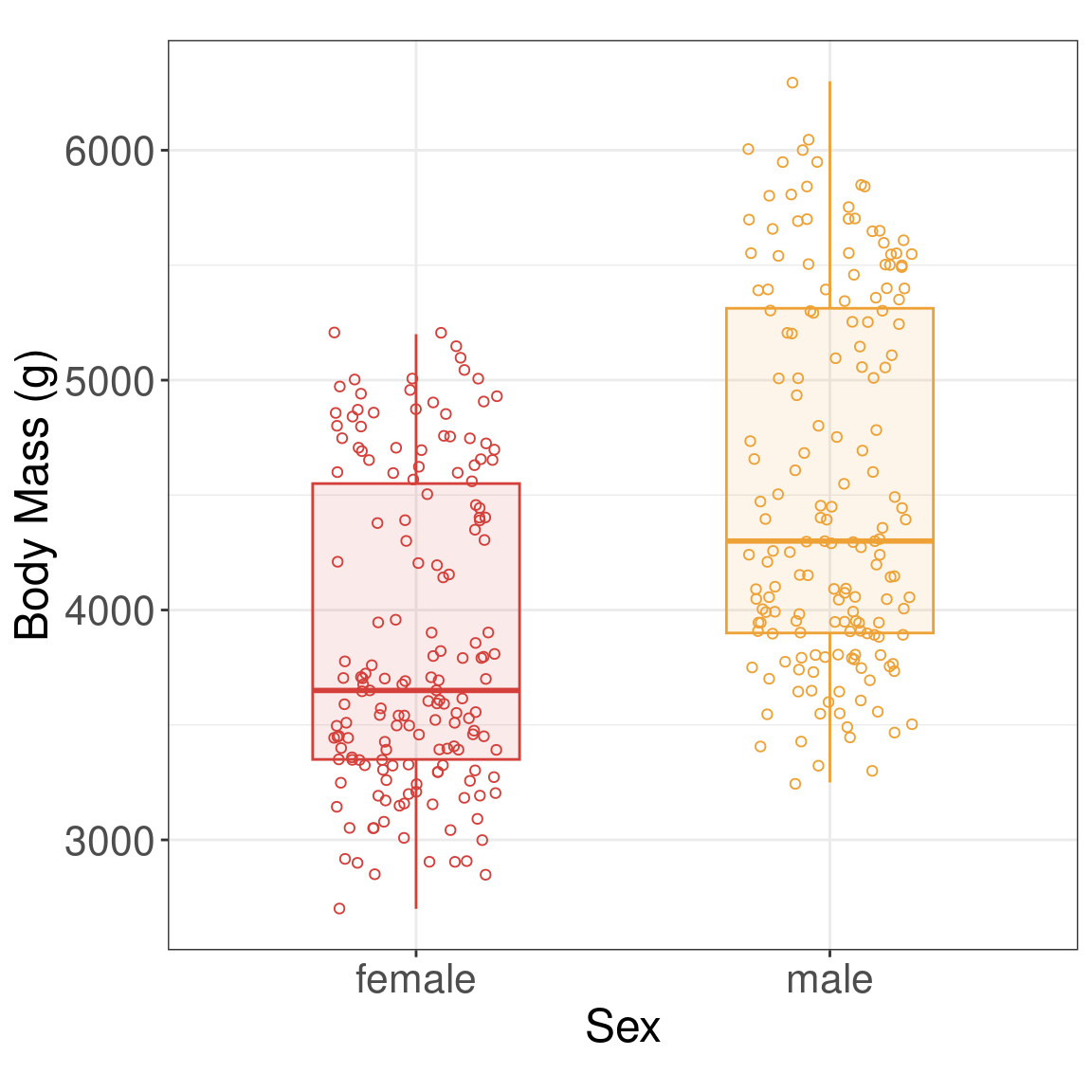
Two-sample t-test

help(t.test)
t.test(y ~ x, 
       data = data_name,
       alternative = “two.sided”, 
       mu = 0, 
       paired = FALSE, 
       var.equal = FALSE, 
       conf.level = 0.95)
  • y: The variable name of the quantitative response.
  • x: The variable name of the grouping variable (or treatment).
  • data: The name of the data set
  • alternative: The alternative hypothesis. Options include “two.sided”, “less”, or “greater.”
  • mu: The value assumed to be the true difference in means.
  • paired: Whether or not to use a paired t-test.
  • var.equal: Whether or not the variances are equal between the two groups.
  • conf.level: The confidence level to use for the test.

Two-sample independent t-test

  • Null: the mean body mass for female penguins is equal to the mean body mass for male penguins (female - male \(= 0\))
  • Alternative: the mean body mass for female penguins is not equal to the mean body mass for male penguins (female - male \(\ne 0\))
penguins_ttest <- t.test(body_mass_g ~ sex, data = penguins2) #<<
penguins_ttest

    Welch Two Sample t-test

data:  body_mass_g by sex
t = -8.5545, df = 323.9, p-value = 4.794e-16
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
 -840.5783 -526.2453
sample estimates:
mean in group female   mean in group male 
            3862.273             4545.685

Two-sample independent t-test (table results)

Extract specific output

penguins_ttest$statistic
penguins_ttest$df
penguins_ttest$p.value

Summarize results with library(broom)

install.packages("broom")
library(broom)
penguins_results <- tidy(penguins_ttest) #<<
penguins_results
estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high method alternative
-683.4 3862.3 4545.7 -8.6 <0.001 323.9 -840.6 -526.2 Welch Two Sample t-test two.sided

Two-sample independent t-test (graphical results)

ggplot(penguins_results, aes(x = NA, y = estimate)) +
  geom_point(size = 2) +
  geom_errorbar(aes(ymin = conf.low, ymax = conf.high), width = 0.2) +
  geom_hline(yintercept = 0, linetype = "dashed", color = "red") +
  theme_bw() +
  theme(aspect.ratio = 0.5, axis.text.y = element_blank()) +
  xlab("") + ylab("Difference in Body Mass \n (Female - Male)") +
  coord_flip()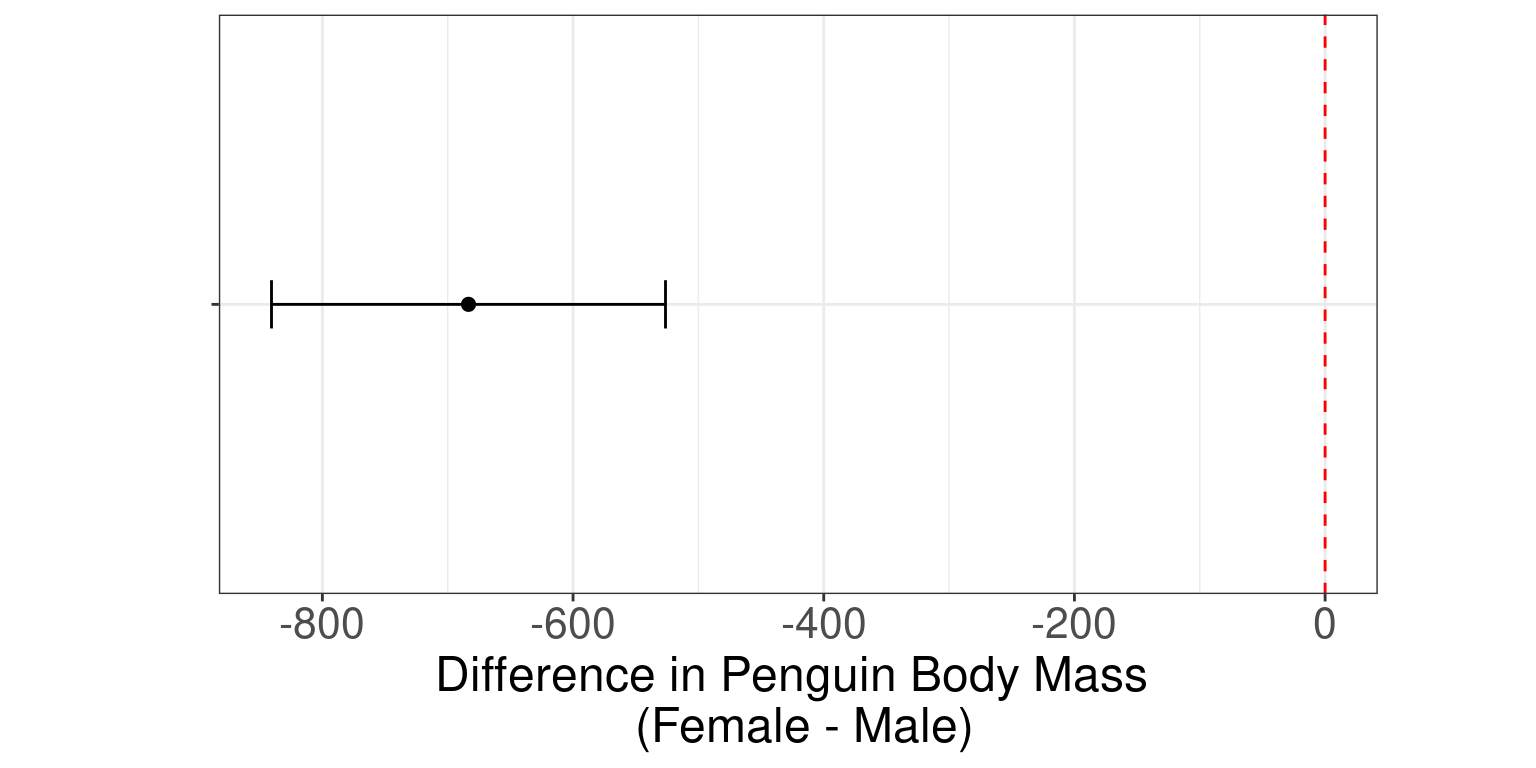

Your Turn

  • What if you wanted the difference to be male - female? (Hint: use relevel())

  • The default confidence level is 95%, how would you change it to a 90% confidence level?

    • Does your p-value change?
    • How about your confidence interval?

Your Turn

  • What if you wanted the difference to be male - female?
levels(penguins2$sex)
[1] "female" "male"  
penguins2$sex <- relevel(penguins2$sex, ref = "male") #<<
levels(penguins2$sex)
[1] "male"   "female"
penguins_ttest2 <- t.test(body_mass_g ~ sex, data = penguins2)
penguins_ttest2
estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high method alternative
683.4 4545.7 3862.3 8.6 <0.001 323.9 526.2 840.6 Welch Two Sample t-test two.sided

Your Turn

  • The default confidence level is 95%, how would you change it to a 90% confidence level?
    • Does your p-value change?
    • How about your confidence interval?
[1] 4.793891e-16
[1] 526.2453 840.5783
attr(,"conf.level")
[1] 0.95
penguins_ttest3 <- t.test(body_mass_g ~ sex, 
                          data = penguins2, 
                          conf.level = 0.9) #<<
penguins_ttest3$p.value
penguins_ttest3$conf.int
[1] 4.793891e-16
[1] 551.6295 815.1941
attr(,"conf.level")
[1] 0.9

Chi-square test of independence

Research Question Are island and the species of penguin associated?

Data

species island
Adelie Torgersen
Adelie Torgersen
Adelie Torgersen



Numerical Summary

           species
island      Adelie Chinstrap Gentoo
  Biscoe        44         0    124
  Dream         56        68      0
  Torgersen     52         0      0

Graphical Summary

Chi-square test of independence

help("chisq.test")
chisq.test(y ~ x, 
       data = data_name,
       simulate.p.value = FALSE,
       B = 2000)

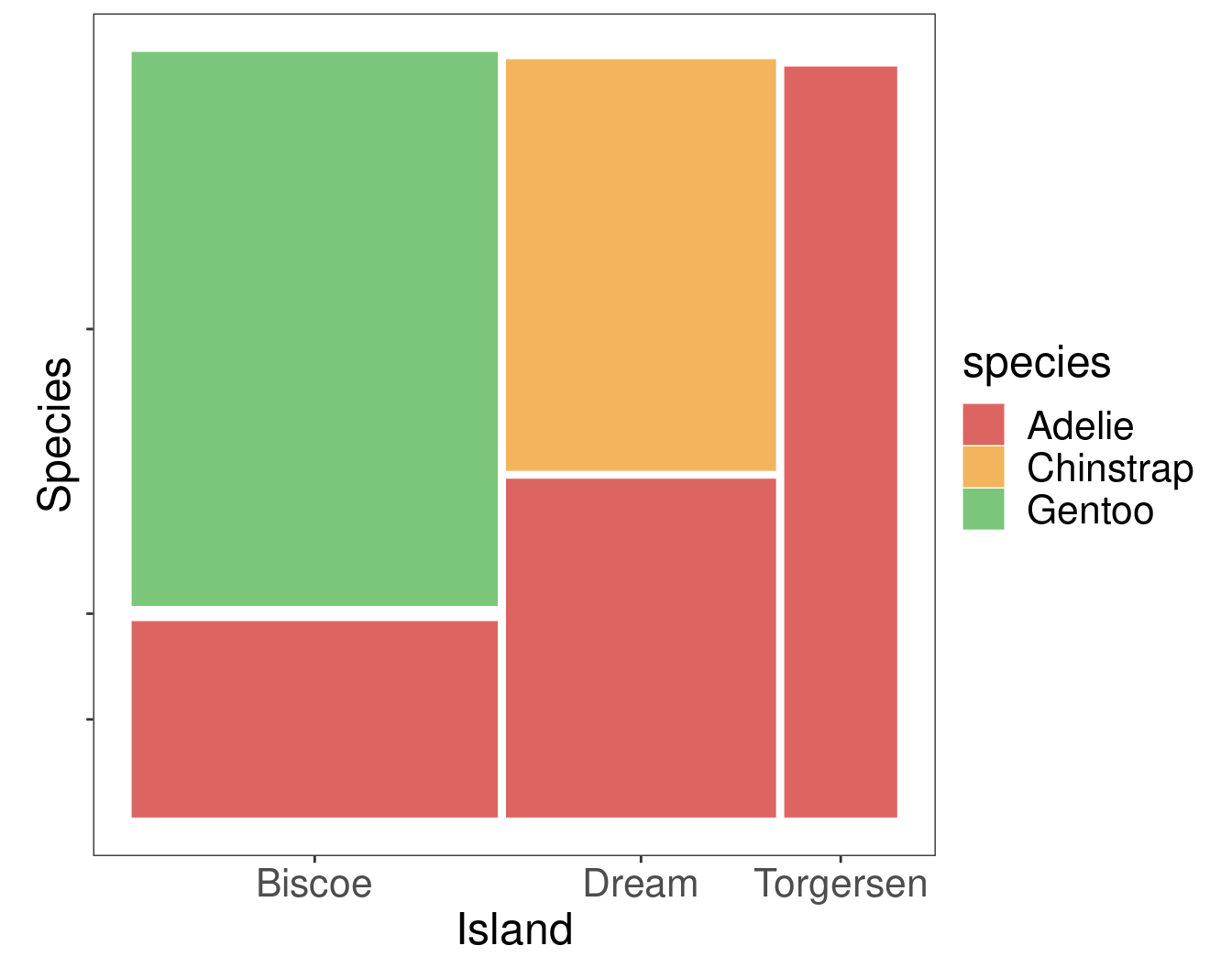
Chi-square test of independence

chisq.test(penguins3$island, penguins3$species) #<<

    Pearson's Chi-squared test

data:  penguins3$island and penguins3$species
X-squared = 299.55, df = 4, p-value < 2.2e-16
chisq.test(penguins3$island, penguins3$species, 
           simulate.p.value = T) #<<

    Pearson's Chi-squared test with simulated p-value (based on 2000
    replicates)

data:  penguins3$island and penguins3$species
X-squared = 299.55, df = NA, p-value = 0.0004998

Simple Regression

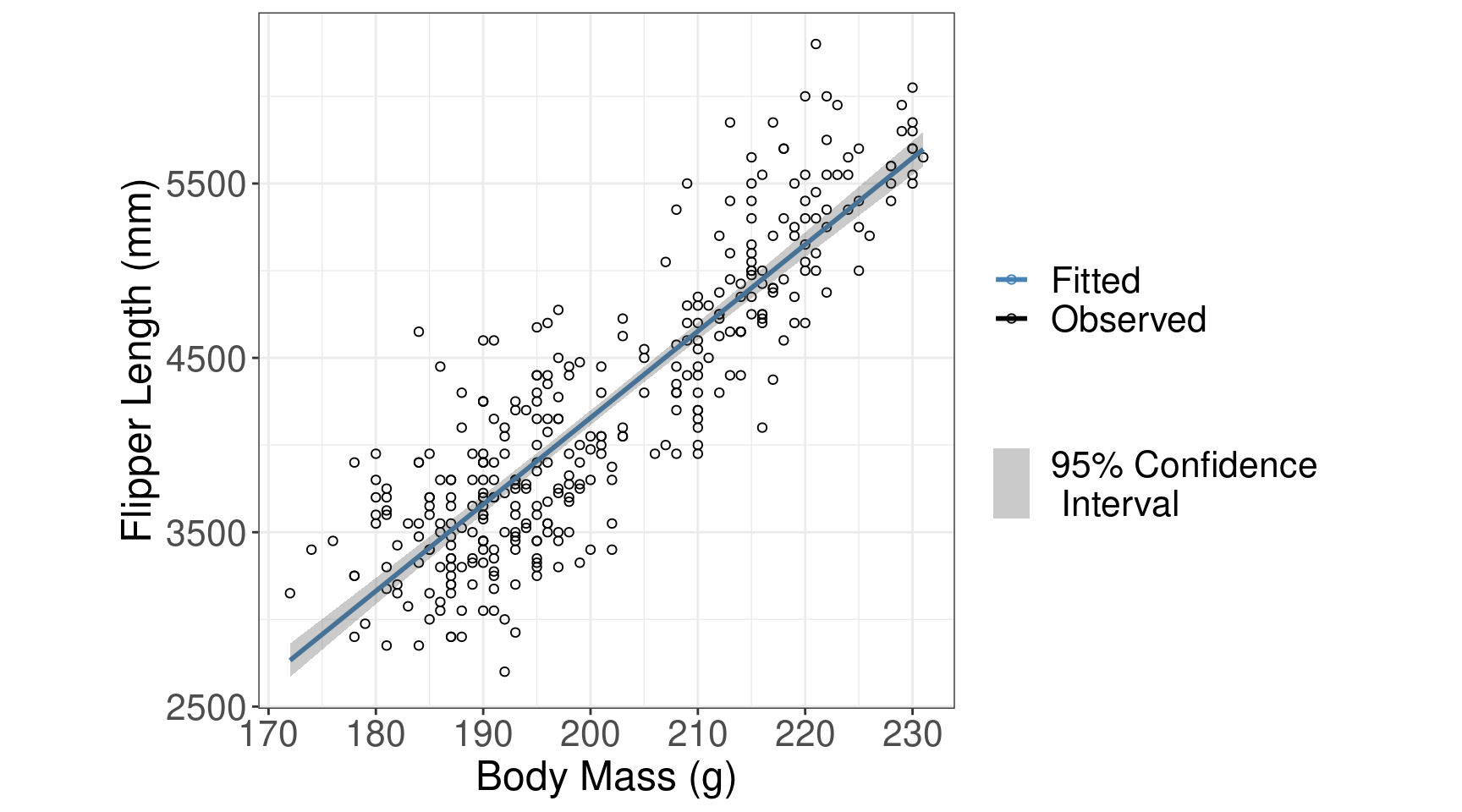
Research Question Is there a relationship between penguin body mass and flipper length?

Data

body_mass_g flipper_length_mm
3750 181
3800 186
3250 195



Numerical Summary

Pearson Correlation

[1] 0.8712018

Graphical Summary

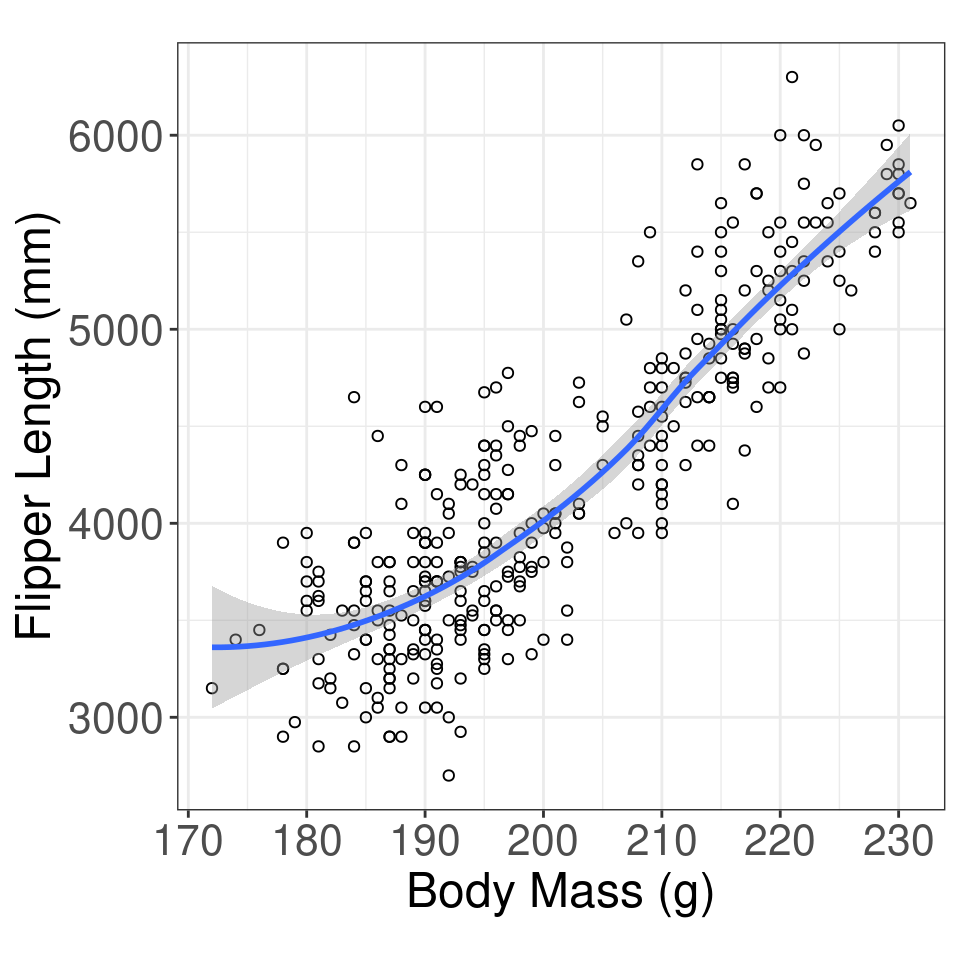
Simple Regression

\[y = \text{intercept} + \text{slope} \cdot x + \text{error}\]

help(lm)
regression_mod <- lm(y ~ x, data = data_name)
summary(regression_mod)

Simple Regression

penguins_regression <- lm(body_mass_g ~ flipper_length_mm, data = penguins4) #<<
summary(penguins_regression)

Call:
lm(formula = body_mass_g ~ flipper_length_mm, data = penguins4)

Residuals:
     Min       1Q   Median       3Q      Max 
-1058.80  -259.27   -26.88   247.33  1288.69 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -5780.831    305.815  -18.90   <2e-16 ***
flipper_length_mm    49.686      1.518   32.72   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 394.3 on 340 degrees of freedom
Multiple R-squared:  0.759, Adjusted R-squared:  0.7583 
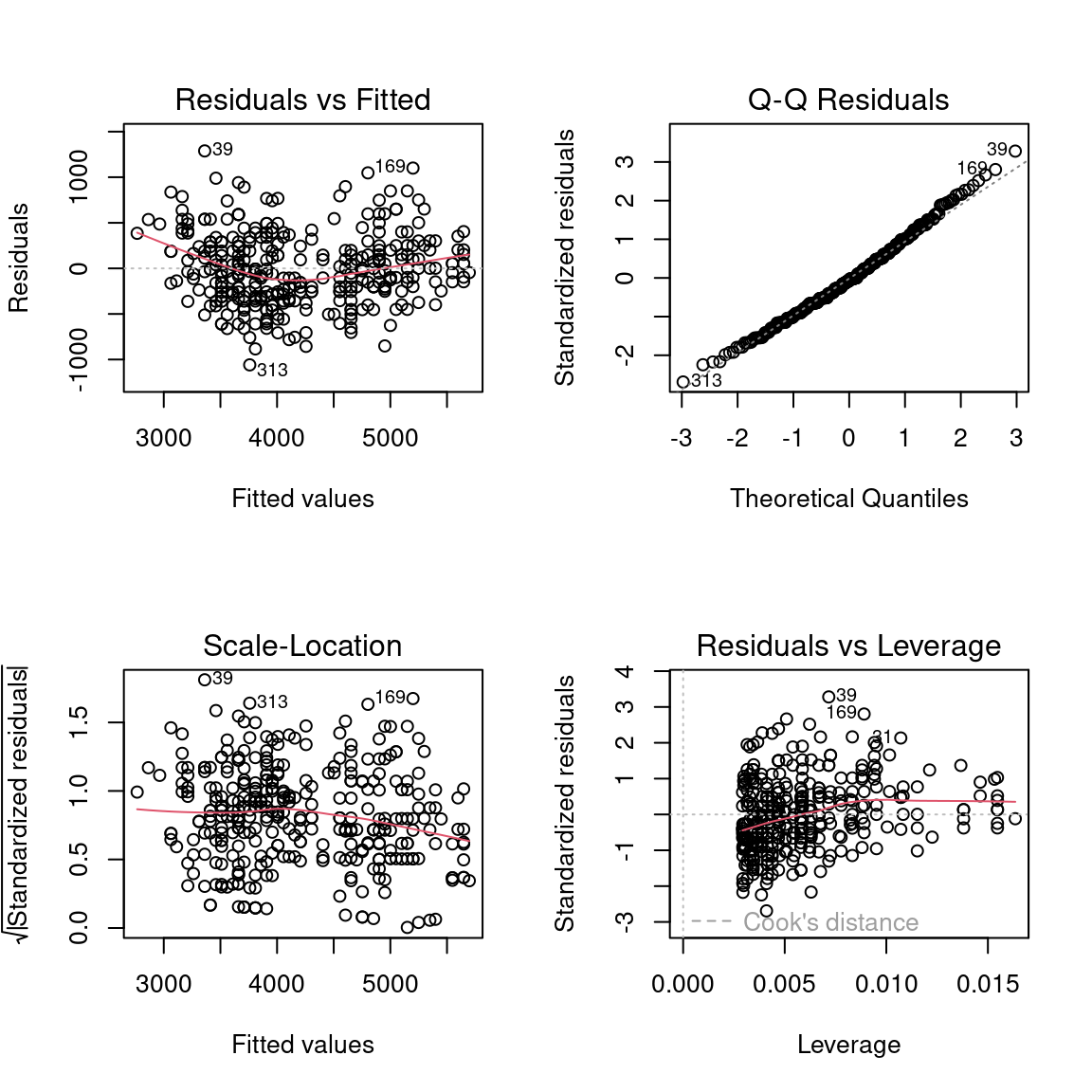
F-statistic:  1071 on 1 and 340 DF,  p-value: < 2.2e-16

Simple Regression (evaluate model)

par(mfrow = c(2,2))
plot(penguins_regression)
par(mfrow = c(1,1))

Simple Regression (results)

\[y_{i} = \beta_0 + \beta_1 \cdot x_{i} + \epsilon_{i}\]

  • \(y_{i}\) is the body mass (g) for penguin \(i = 1, ..., n\)
  • \(\beta_0\) is the intercept coefficient
  • \(\beta_1\) is the slope coefficient
  • \(x_{i}\) is the flipper length (mm) for penguin \(i = 1, ..., n\)
  • \(\epsilon_i\) is the error for penguin \(i = 1, ..., n\) where \(\epsilon \sim N(0, \sigma^2)\)
tidy(penguins_regression)  %>% 
  mutate(p.value = scales::pvalue(p.value))
term estimate std.error statistic p.value
(Intercept) -5780.83 305.81 -18.90 <0.001
flipper_length_mm 49.69 1.52 32.72 <0.001

\(\text{body mass}_{i} = -5780.83 + 49.56 \cdot \text{flipper length}_{i} + \epsilon_{i}\) where \(\epsilon \sim N(0, \sigma^2)\)

Simple Regression (results)

term estimate std.error statistic p.value
(Intercept) -5780.83 305.81 -18.90 <0.001
flipper_length_mm 49.69 1.52 32.72 <0.001


Hypotheses

\[H_0: \beta_1 = 0 \text{ (the slope is equal to 0)}\] \[H_A: \beta_1 \ne 0 \text{ (the slope is not equal to 0)}\]


Conclusion

We have evidence to conclude there is an association between flipper length and body mass (t = 32.72; df = 340; p < 0.0001).

Simple Regression (results)

penguins_preds <- cbind(penguins4, predict(penguins_regression, interval = 'confidence')) #<<
ggplot(penguins_preds, aes(x = flipper_length_mm, y = body_mass_g)) +
  geom_point(shape = 1) +
  geom_line(aes(y = fitted(penguins_regression))) + #<<
  geom_ribbon(aes(ymin = lwr, ymax = upr), alpha = 0.3)  #<<

Your Turn: Simple Regression

Fit a linear regression line between bill length and bill depth for each species

UNL R Workshops