Generalized Linear Models (and more!)

Outline

  • What if my response does not follow a normal distribution?

  • Binomial Example

  • Count Example

  • Final Remarks

Generalized Linear Models (Basics)

If your data is not normally distributed, it will violate the model assumptions of a linear model. You must consider the type of data you have!

Model Scale verses Data Scale

Common Distributions

  • Binomial (binary data or number of successes out of total)

  • Poisson (count data)

  • Negative Binomial (count data)

  • Gamma (right skewed continuous data)

  • Beta (continuous proportion/probability)

GLMS and GLMM’s in R

Packages

library('lme4')
library('emmeans')

Generalized Linear Model (GLM)

help(glm)

Generalized Linear Mixed Model (GLMM)

help(glmer)

Binomial Example

Insects

Data The number of insects killed at various doses of insecticide.

insects_data <- read_csv("https://unl-statistics.github.io/R-workshops/r-modeling/data/insects.csv")
head(insects_data)
Rep Killed Number Insecticide Deposit
1 3 50 A 2.00
1 5 49 A 2.64
1 19 47 A 3.48
1 19 38 A 4.59
  • Killed the number of insects killed at each poison level; a numeric vector
  • Number the number of insects exposed at each poison level; a numeric vector
  • Insecticide the insecticide used; a factor with levels A, B and C
  • Deposit the amount of deposit (insecticide) used in milligrams; a numeric vector

Insects EDA

 Rep        Killed          Number      Insecticide    Deposit     
 1:18   Min.   : 1.00   Min.   :26.00   A:18        Min.   :2.000  
 2:18   1st Qu.:17.00   1st Qu.:48.00   B:18        1st Qu.:2.640  
 3:18   Median :29.00   Median :50.00   C:18        Median :4.035  
        Mean   :27.78   Mean   :47.48               Mean   :4.462  
        3rd Qu.:40.75   3rd Qu.:50.00               3rd Qu.:6.060  
        Max.   :50.00   Max.   :50.00               Max.   :8.000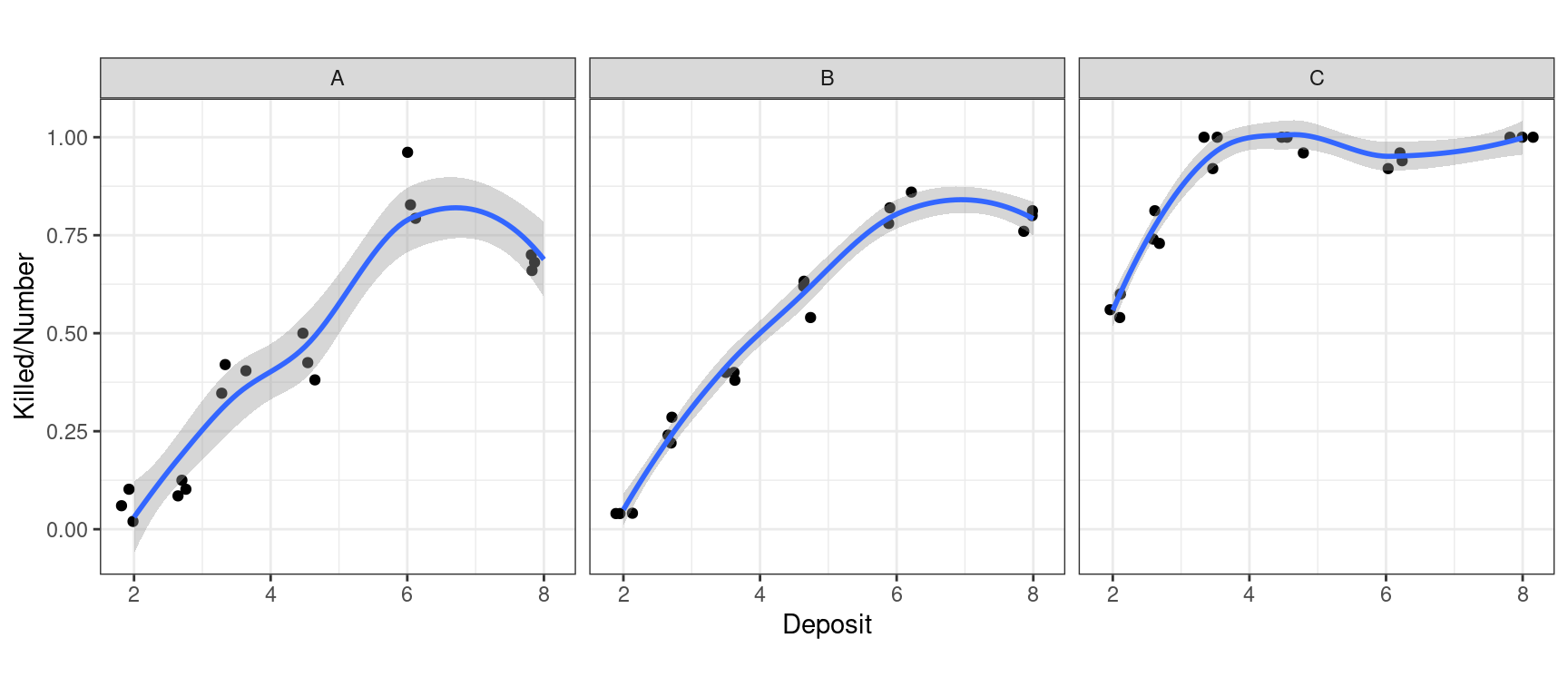


Insects Model

Statistical notation

\[y_{ij} \sim \text{Binomial}(\pi_{ij}, N_{ij})\] where \[\log\large(\frac{\pi_{ij}}{1-\pi_{ij}}\large) = \eta_{ij} = (\beta_0 + \tau_i) + (\beta_1 + \beta_{1i})\cdot x_{ij} + (\beta_2 + \beta_{2i})\cdot x_{ij}^2\]

  • \(y_{ij}\) is the number of insects killed for the \(i^{th}\) Insecticide given the \(j^{th}\) deposit.

  • \(N_{ij}\) is the total number of insects that started.

  • \(\eta\) is the overall mean on the model scale.

  • \(\tau_i\) is the effect of the \(i^{th}\) habitat.

  • \(b_j\) is the random variation due to the \(j^{th}\) site.

  • \(logit = \log(\frac{\pi}{1-\pi})\) data scale \(\implies\) model scale (link function)

  • \(\frac{1}{(1+e^{-\eta})}\) model scale \(\implies\) data scale (ilink function)

Insects GLM

 insects_glm <- glm(Killed/Number ~ Insecticide*Deposit + Insecticide*I(Deposit^2),
     weights = Number, #<<
     data = insects_data,
     family = "binomial") #<<
car::Anova(insects_glm)
Analysis of Deviance Table (Type II tests)

Response: Killed/Number
                         LR Chisq Df Pr(>Chisq)    
Insecticide                639.65  2     <2e-16 ***
Deposit                    197.82  1     <2e-16 ***
I(Deposit^2)               104.08  1     <2e-16 ***
Insecticide:Deposit          0.28  2     0.8711    
Insecticide:I(Deposit^2)     0.30  2     0.8612    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Insects GLM

summary(insects_glm)

Call:
glm(formula = Killed/Number ~ Insecticide * Deposit + Insecticide * 
    I(Deposit^2), family = "binomial", data = insects_data, weights = Number)

Coefficients:
                           Estimate Std. Error z value Pr(>|z|)    
(Intercept)               -6.913880   0.687916 -10.050  < 2e-16 ***
InsecticideB               0.676798   0.911342   0.743  0.45770    
InsecticideC               3.053194   1.010612   3.021  0.00252 ** 
Deposit                    2.371302   0.287991   8.234  < 2e-16 ***
I(Deposit^2)              -0.175414   0.026636  -6.586 4.53e-11 ***
InsecticideB:Deposit      -0.154556   0.385324  -0.401  0.68834    
InsecticideC:Deposit       0.066789   0.498966   0.134  0.89352    
InsecticideB:I(Deposit^2)  0.016766   0.036163   0.464  0.64292    
InsecticideC:I(Deposit^2) -0.005033   0.052369  -0.096  0.92344    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1326.798  on 53  degrees of freedom
Residual deviance:   86.522  on 45  degrees of freedom
AIC: 278.27

Number of Fisher Scoring iterations: 5

Insects results

insects_emmeangrid <- ref_grid(insects_glm, at = list(Deposit = unique(insects_data$Deposit))) #<<
insects_emmeans <- emmeans(insects_emmeangrid, specs =~Insecticide:Deposit, type = "response")
insects_emmeans
Insecticide Deposit prob SE df asymp.LCL asymp.UCL
A 2.00 0.054 0.012 Inf 0.034 0.083
B 2.00 0.080 0.015 Inf 0.055 0.116
C 2.00 0.573 0.037 Inf 0.499 0.643
A 2.64 0.133 0.018 Inf 0.102 0.172
B 2.64 0.184 0.020 Inf 0.148 0.226
C 2.64 0.789 0.020 Inf 0.746 0.826

Compare Insecticides

insects_pairs <- emmeans(insects_emmeangrid, specs =~Insecticide | Deposit, type = "response")
pairs(insects_pairs, infer = c(T,T))
Deposit = 2:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.6474 0.20481 Inf   0.30846    1.3589    1  -1.374  0.3544
 A / C        0.0421 0.01198 Inf   0.02165    0.0820    1 -11.141  <.0001
 B / C        0.0651 0.01661 Inf   0.03580    0.1184    1 -10.707  <.0001

Deposit = 2.64:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.6800 0.13910 Inf   0.42104    1.0983    1  -1.885  0.1429
 A / C        0.0410 0.00809 Inf   0.02581    0.0651    1 -16.184  <.0001
 B / C        0.0603 0.01091 Inf   0.03944    0.0921    1 -15.525  <.0001

Deposit = 3.48:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.7104 0.10409 Inf   0.50388    1.0015    1  -2.334  0.0513
 A / C        0.0398 0.00892 Inf   0.02351    0.0673    1 -14.375  <.0001
 B / C        0.0560 0.01229 Inf   0.03347    0.0936    1 -13.132  <.0001

Deposit = 4.59:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.7257 0.12800 Inf   0.47999    1.0972    1  -1.818  0.1637
 A / C        0.0386 0.01159 Inf   0.01912    0.0780    1 -10.843  <.0001
 B / C        0.0532 0.01568 Inf   0.02669    0.1061    1  -9.960  <.0001

Deposit = 6.06:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.7005 0.13204 Inf   0.45039    1.0896    1  -1.888  0.1421
 A / C        0.0379 0.01316 Inf   0.01679    0.0855    1  -9.424  <.0001
 B / C        0.0541 0.01847 Inf   0.02429    0.1204    1  -8.542  <.0001

Deposit = 8:
 contrast odds.ratio      SE  df asymp.LCL asymp.UCL null z.ratio p.value
 A / B        0.5985 0.15779 Inf   0.32261    1.1102    1  -1.947  0.1257
 A / C        0.0382 0.02450 Inf   0.00849    0.1717    1  -5.090  <.0001
 B / C        0.0638 0.04130 Inf   0.01399    0.2909    1  -4.251  0.0001

Confidence level used: 0.95 
Conf-level adjustment: tukey method for comparing a family of 3 estimates 
Intervals are back-transformed from the log odds ratio scale 
P value adjustment: tukey method for comparing a family of 3 estimates 
Tests are performed on the log odds ratio scale

Insects results plot

insects_predgrid <- ref_grid(insects_glm, at = list(Deposit = seq(min(insects_data$Deposit), max(insects_data$Deposit), 0.2)))
insects_preds <- emmeans(insects_predgrid, specs =~Insecticide:Deposit, type = "response")
insects_preds
Insecticide Deposit prob SE df asymp.LCL asymp.UCL
A 2.0 0.054 0.012 Inf 0.034 0.083
B 2.0 0.080 0.015 Inf 0.055 0.116
C 2.0 0.573 0.037 Inf 0.499 0.643
A 2.2 0.073 0.014 Inf 0.049 0.106
B 2.2 0.106 0.017 Inf 0.077 0.145
C 2.2 0.652 0.029 Inf 0.594 0.707

Insects results plot

insects_preds %>%
  as_tibble() %>%
  ggplot(aes(x = Deposit, shape = Insecticide, color = Insecticide, fill = Insecticide)) +
  geom_line(aes(y = prob)) + #<<
  geom_ribbon(aes(ymin = asymp.LCL, ymax = asymp.UCL), color = NA, alpha = 0.2) + #<<
  geom_point(data = insects_data, aes(y = Killed/Number), position = position_jitter(width = 0.2, height = 0)) + #<<
  theme_bw() +
  theme(aspect.ratio = 1) +
  scale_color_locuszoom() +
  scale_fill_locuszoom() +
  scale_y_continuous("Mortality (%)", labels = scales::percent)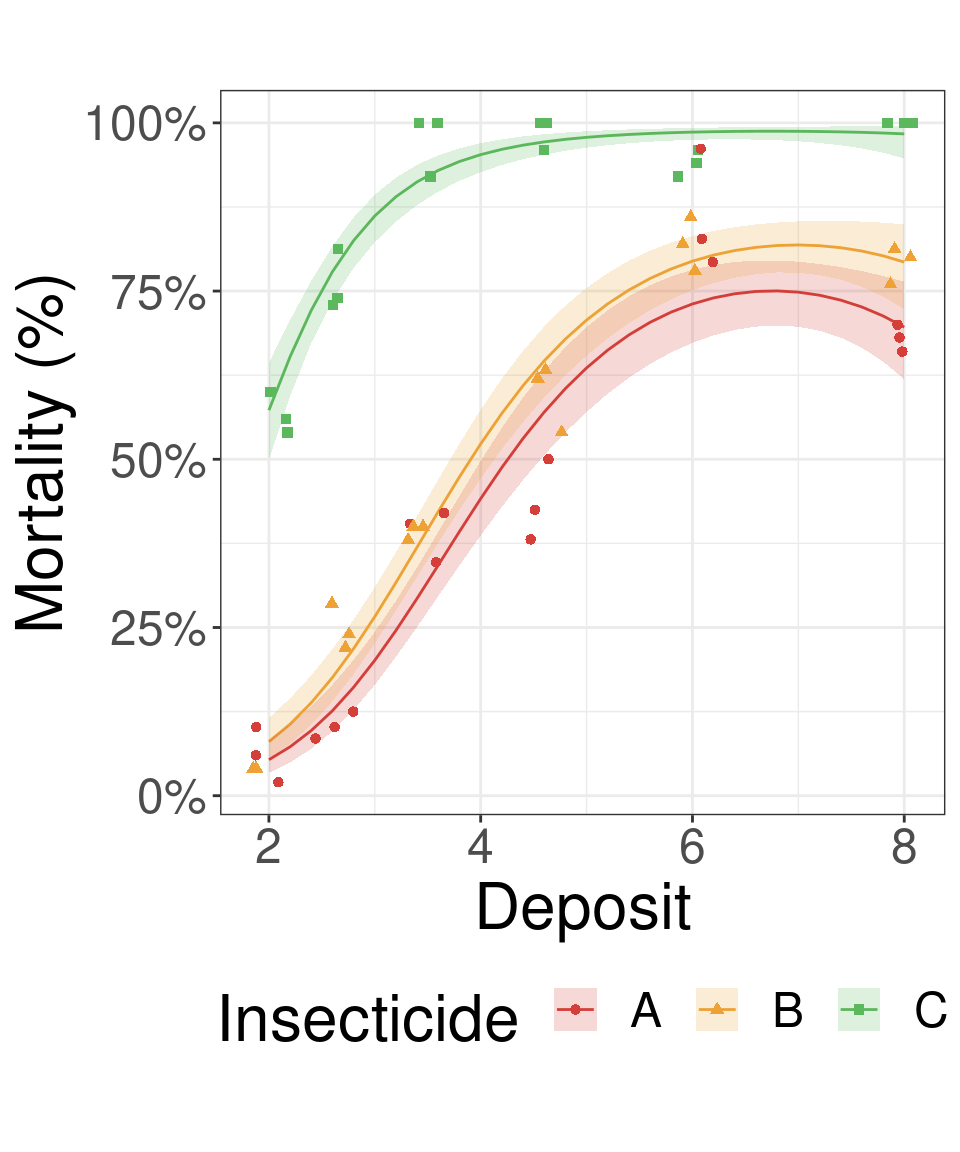

Count Example

Birds

An ecologist is investigating the impact of habitat type on the population of a certain type of bird. To do this, data were obtained from a study in which 24 randomly sampled sites were observed. Each site contains habitats of both types. Bird counts were obtained from each habitat type.

birds_data <- read_csv("https://unl-statistics.github.io/R-workshops/r-modeling/data/birds.csv")
head(birds_data)
Site Habitat Count
1 1 27
1 2 209
2 1 1
2 2 0
3 1 12
3 2 21

Birds EDA

summary(birds_data)
      Site          Habitat        Count       
 Min.   : 1.00   Min.   :1.0   Min.   :  0.00  
 1st Qu.: 6.75   1st Qu.:1.0   1st Qu.:  6.75  
 Median :12.50   Median :1.5   Median : 18.00  
 Mean   :12.50   Mean   :1.5   Mean   : 76.83  
 3rd Qu.:18.25   3rd Qu.:2.0   3rd Qu.: 51.50  
 Max.   :24.00   Max.   :2.0   Max.   :989.00  
factorCols <- c("Site", "Habitat")
birds_data[,factorCols] <- lapply(birds_data[,factorCols], factor)
summary(birds_data)
      Site    Habitat     Count       
 1      : 2   1:24    Min.   :  0.00  
 2      : 2   2:24    1st Qu.:  6.75  
 3      : 2           Median : 18.00  
 4      : 2           Mean   : 76.83  
 5      : 2           3rd Qu.: 51.50  
 6      : 2           Max.   :989.00  
 (Other):36

Birds EDA

Data Scale

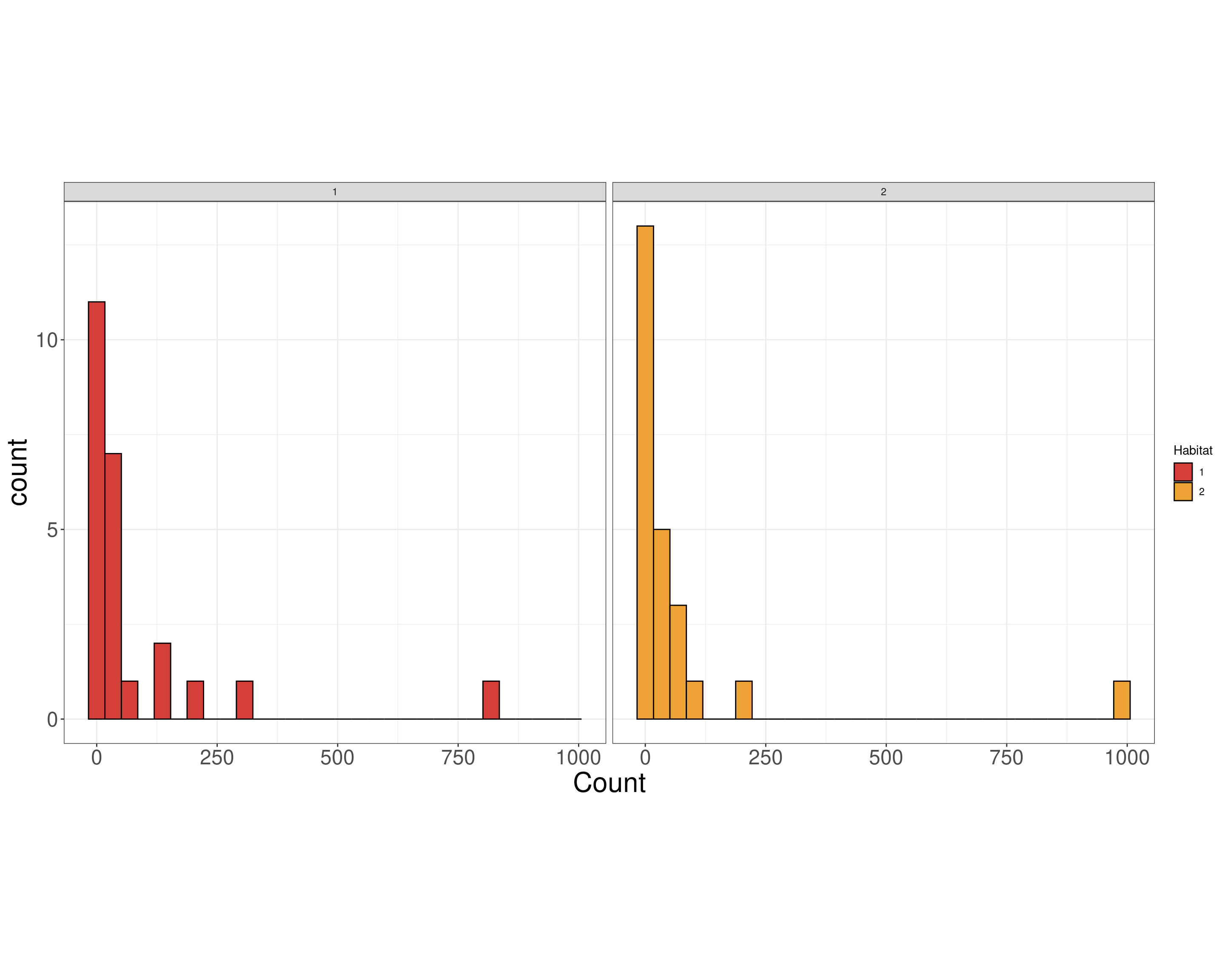
“Model Scale”

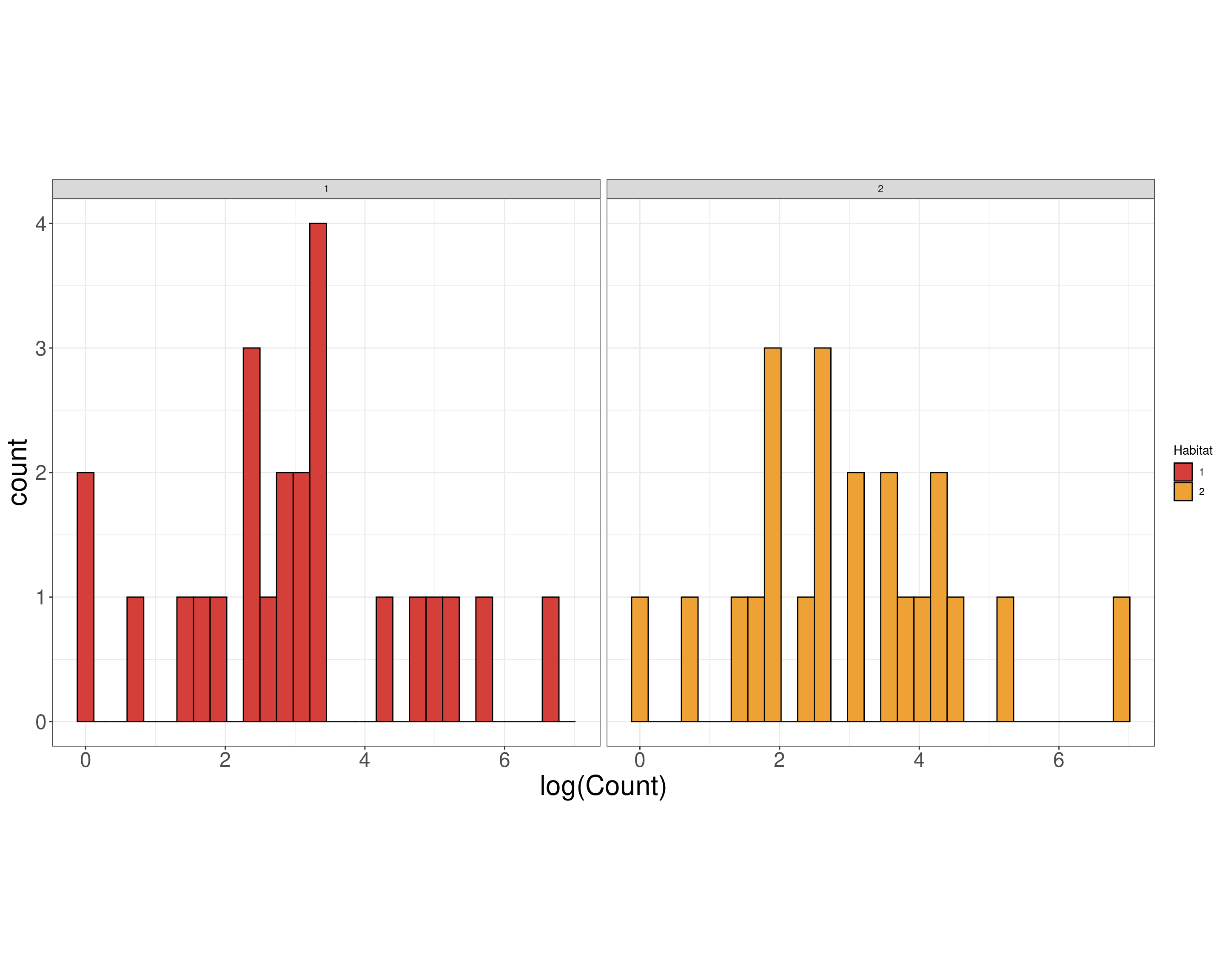
Birds Model

In words

\[\text{"log(Bird Count) = overall model scale mean + habitat + random site + scale"}\]

Statistical notation

\[y_i | b_j \sim \text{Negative Binomial}(\mu_{ij}, \phi)\] where \[\log(\mu_{ij}) = \eta_{ij} = \eta + \tau_i + b_j\]

  • \(y_{ij}\) is bird count for the \(i^{th}\) habitat at the \(j^{th}\) site.

  • \(\eta\) is the overall mean on the model scale.

  • \(\tau_i\) is the effect of the \(i^{th}\) habitat.

  • \(b_j\) is the random variation due to the \(j^{th}\) site.

  • log: data scale \(\implies\) model scale (link function)

  • exp: model scale \(\implies\) data scale (ilink function)

Birds GLMM

library(optimx)
birds_nb <- glmer.nb(Count ~ Habitat + (1|Site),
                     data = birds_data,
                     nAGQ = 100)
car::Anova(birds_nb)
Analysis of Deviance Table (Type II Wald chisquare tests)

Response: Count
         Chisq Df Pr(>Chisq)
Habitat 0.0095  1     0.9224

Birds GLMM results

summary(birds_nb)
Generalized linear mixed model fit by maximum likelihood (Adaptive
  Gauss-Hermite Quadrature, nAGQ = 100) [glmerMod]
 Family: Negative Binomial(0.0849)  ( log )
Formula: Count ~ Habitat + (1 | Site)
   Data: birds_data

     AIC      BIC   logLik deviance df.resid 
    20.9     28.4     -6.5     12.9       44 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-0.2912 -0.2663 -0.2262 -0.0861  3.6476 

Random effects:
 Groups Name        Variance  Std.Dev. 
 Site   (Intercept) 1.444e-12 1.202e-06
Number of obs: 48, groups:  Site, 24

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   4.3888     0.7009   6.262  3.8e-10 ***
Habitat2     -0.0966     0.9912  -0.097    0.922    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
         (Intr)
Habitat2 -0.707
optimizer (Nelder_Mead) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')

Birds GLMM means

birds_emmeans <- emmeans(birds_nb, specs = ~ Habitat, 
                         type = "response") #<<
birds_emmeans
Habitat response SE df asymp.LCL asymp.UCL
1 80.54 56.45 Inf 20.39 318.12
2 73.13 51.25 Inf 18.51 288.85

Birds GLMM compare habitats

\[H_0: \mu_1 = \mu_2 \text{ (The mean bird count for habitat 1 is equal to habitat 2)}\]

\[H_A: \mu_1 \ne \mu_2 \text{ (The mean bird count for habitat 1 is not equal to habitat 2)}\]

pairs(birds_emmeans, infer = c(T,T))
 contrast            ratio   SE  df asymp.LCL asymp.UCL null z.ratio p.value
 Habitat1 / Habitat2   1.1 1.09 Inf     0.158      7.69    1   0.097  0.9224

Confidence level used: 0.95 
Intervals are back-transformed from the log scale 
Tests are performed on the log scale

Birds GLMM compare habitats

\[H_0: \mu_1 = \mu_2 \text{ (The mean bird count for habitat 1 is equal to habitat 2)}\]

\[H_A: \mu_1 \ne \mu_2 \text{ (The mean bird count for habitat 1 is not equal to habitat 2)}\]

library(multcomp)
library(multcompView)
library(stringr)
birds_letters <- cld(birds_emmeans, Letters = letters, alpha = 0.5) %>% #<<
  mutate(.group = toupper(str_trim(.group))) #<<
birds_letters
Habitat response SE df asymp.LCL asymp.UCL .group
2 73.13 51.25 Inf 18.51 288.85 A
1 80.54 56.45 Inf 20.39 318.12 A

Count Example: Birds results plot

birds_letters %>%
  as_tibble() %>% #<<
  ggplot(aes(x = Habitat, y = response)) +
  geom_point() +
  geom_errorbar(aes(ymin = asymp.LCL, ymax = asymp.UCL), width = 0.1) +
  geom_text(aes(label = .group, y = asymp.UCL), vjust = -0.5, size = 6) + #<<
  geom_point(data = birds_data, aes(y = Count), shape = 1, position = position_jitter(width = 0.2, height = 0)) + #<<
  theme_bw() +
  theme(aspect.ratio = 1) +
  ylab("Number of Birds")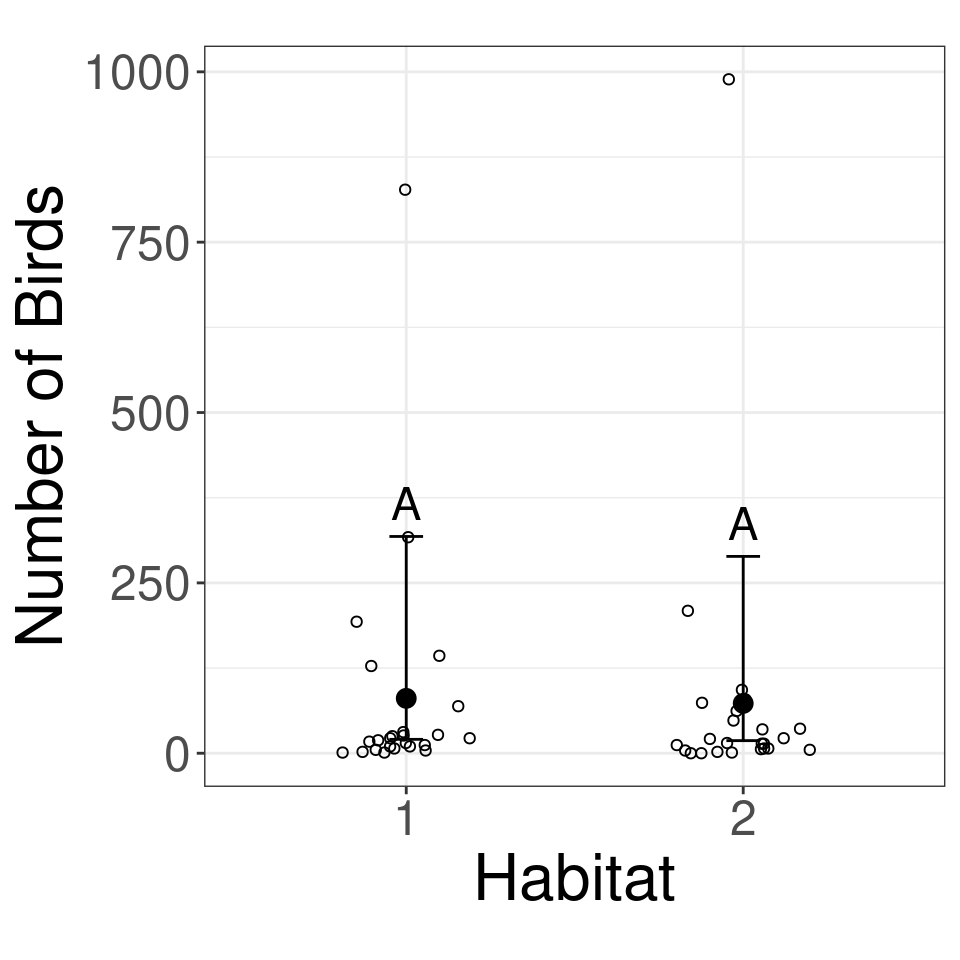

Final Remarks

Models and functions

Model Distribution Experimental Design R Function
Linear Model Normal CRD lm()
Linear Mixed Model Normal Blocking (or more) lmer()
Generalized Linear Model Non-normal CRD glm()
Generalized Linear Mixed Model Non-normal Blocking (or more) glmer()

Model Specifications

Image source: https://bbolker.github.io/mixedmodels-misc/glmmFAQ.html

Additional models and functions

Repeated Measures

  • Take multiple measures on the same object over a period of time
  • lme() in nlme package

Nonlinear Regression

  • Does not follow the typical polynomial framework
  • nls() in base R, stats package

Generalized Additive Models (GAM)

  • Estimates smoothing splines
  • gam() in mcgv package

UNL R Workshops