Countering Statistical Misconceptions

Types of Misconceptions

  • 🗺️ General misconceptions about statistics

  • 🧑‍🔬 🧑‍💼 Subject-matter expert (SME) misconceptions about statistics

  • 🤵🕴️ Manager misconceptions

General Statistical Misconceptions

General Statistical Misconception Examples

Harvey J. Motulsky “Common Misconceptions about Data Analysis and Statistics,” Naunyn-Schmiedeberg’s Archives of Pharmacology 387, no. 11 (2014): 1017–23, https://doi.org/10.1007/s00210-014-1037-6.

  • Correlation => Causation

  • Linear regression is the only regression

  • Small p-value = big effect size

  • \(R^2\) must be \(>0.95\) to matter

Correlation and Causation

Samuel J. Gershman and Tomer D. Ullman “Causal Implicatures from Correlational Statements,” PLOS ONE 18, no. 5 (May 18, 2023): e0286067, https://doi.org/10.1371/journal.pone.0286067.

  • People infer causation from correlational statements, using the variable order as a directional indicator

    • Even with “X is associated with an increased risk of Y” language
    • Even when given the choice of non-causal interpretations, 47% of people still use causal interpretations

In summary, certain correlational statements are associated with an increased probability of causal implicature. To be clear, we are not implying that these correlational statements cause causal implicature, but rather that they are correlated with causal implicature. In other words, correlation does not imply causation, but it does sometimes “imply” causation.

Regression

📐 Engineers

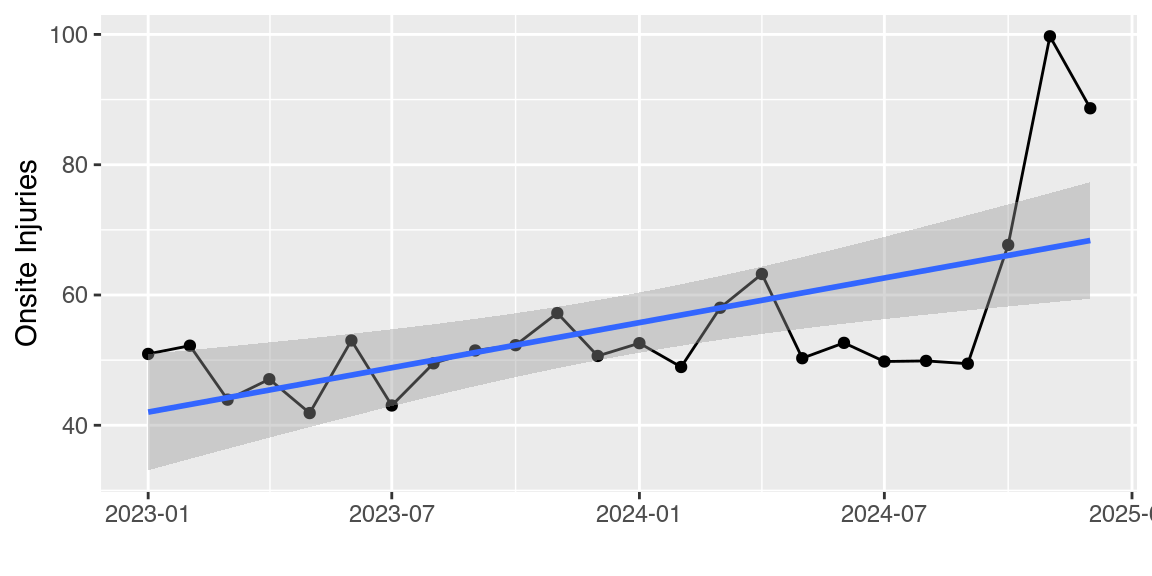
A chart showing on site injuries for the 24 month period starting in January 2023. The last 3 observations are elevated compared to the previous 21. A linear regression line is overlaid showing an increase in injuries during the period.

  • “Oh no, there’s been a huge increase in injuries! We need to do something now, before the problem gets worse!”

🤣 Statisticians

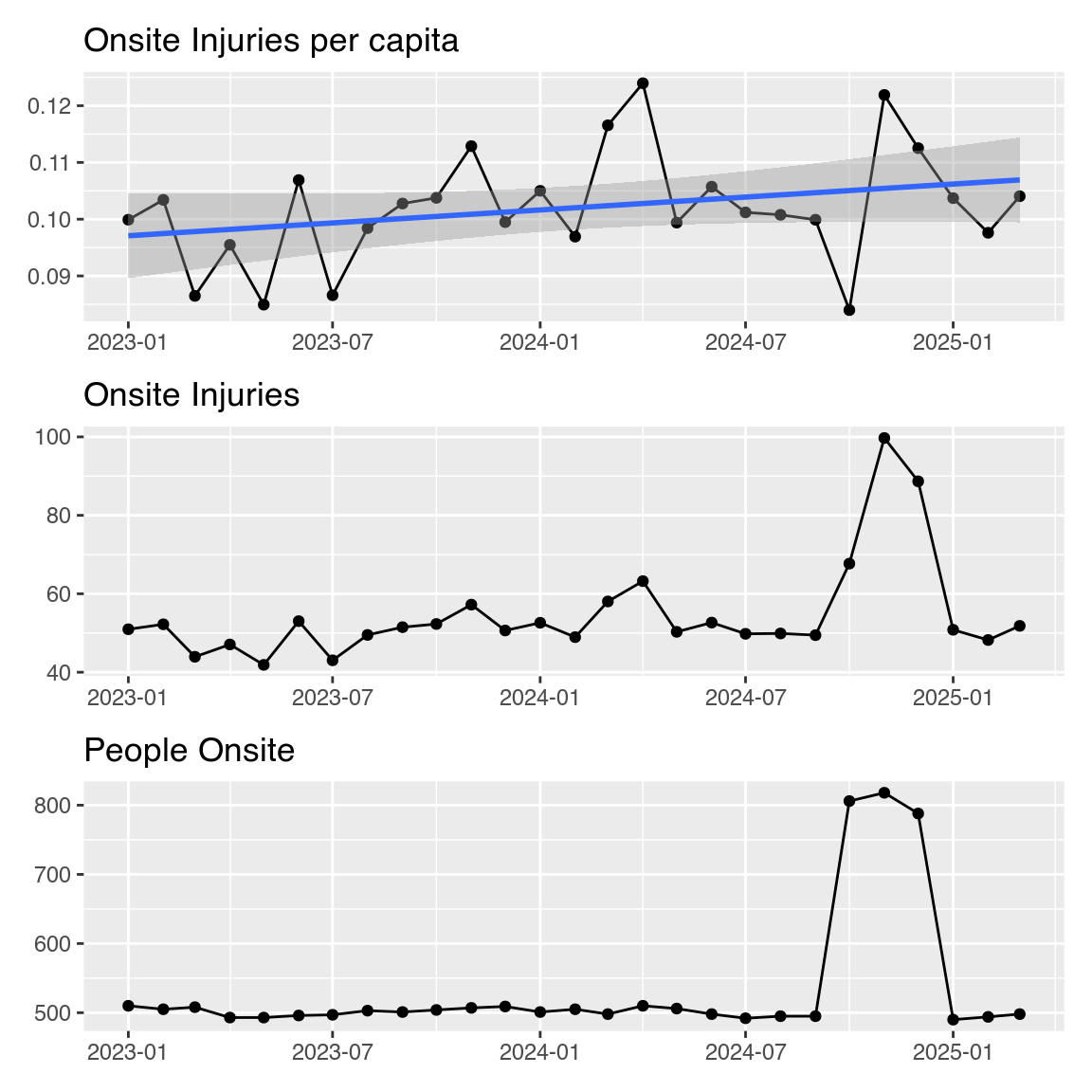
A set of three charts showing on site injuries per capita, on site injuries, and people on site for the 27 month period starting in January 2023. There are 3 observations of on site injuries starting in Oct 2025 which are elevated compared to the previous 21; the last 3 observations show a return to baseline. A similar increase in number of people onsite is shown, and per capita injuries is largely unchanged.

  • linear regression isn’t the right tool for this

  • have you considered other explanations?

  • let’s add more data…

P-values

Misconception: Small p-value => Bigger effect size

T-test between \(x_1 \sim N(0, 1)\) and \(x_2 \sim N(1, 1)\)

True \(\mu_2-\mu_1 = 1\), \(\eta = 1\)

Two histograms showing p-values for 500 simulations of 50 samples per group, with a mean difference between groups of 0 (left) and 1 (right). On the left, the p-values are approximately uniformly distributed, with 0-10 observations for each of 100 bars. On the right, almost all observations are in the left-most bucket corresponding to [0, 0.01].

Under \(H_0\), p-values are uniform(0, 1) distributed!

Within each panel, the effect size is the same.

P-values

Misconception: Small p-value => Bigger effect size

T-test between \(x_1 \sim N(0, 0.5)\) and \(x_2 \sim N(0.5, 0.5)\)

True \(\mu_2-\mu_1 = 0.5\), \(\eta = 1\)

Two histograms showing p-values for 500 simulations of 50 samples per group, with a mean difference between groups of 0 (left) and 2 (right). On the left, the p-values are approximately uniformly distributed, with 0-10 observations for each of 100 bars. On the right, all observations are in the left-most bucket corresponding to [0, 0.01].

R^2

  • As number of predictors increases in multiple regression, \(R^2\) only increases. Adjusted \(R^2\) accounts for this issue.

  • Good \(R^2\) are different for different fields…

R^2

  • \(R^2\) only measures linear relationships

  • Not all interesting relationships are linear

SME Misconceptions

Kenneth J. Rothman, “Six Persistent Research Misconceptions,” Journal of General Internal Medicine 29, no. 7 (January 23, 2014): 1060–64, https://doi.org/10.1007/s11606-013-2755-z.

  • Randomized trials are more valid than cohort or case-control studies

  • Study subjects must be a representative sample of the target population for generalizations to be made

  • Lack of statistical interaction = lack of biological interaction

  • Categorizing a continuous variable by percentiles is a good idea

  • Significance testing is the best way to report results

Randomized Trials

  • Randomized trials still have divergent results

    • random error

    • systematic errors (bias) - undercounting, missing data, non-adherence (e.g. medical studies)

  • Well-controlled cohort studies have some advantages:

    • age control

    • time since diagnosis of a condition may be better controlled

Simpson’s paradox can explain a lot of these issues!

Simpson’s Paradox

Kidney stone treatment experiment: Treatments A and B. Recorded stone size (large, small) and outcome of the treatment (success, failure).

Two mosaic plots, one which shows Outcome and Treatment

Failure to account for moderating variables can lead to the opposite (wrong) conclusion!

Make sure your model uses the available data

Representative Samples

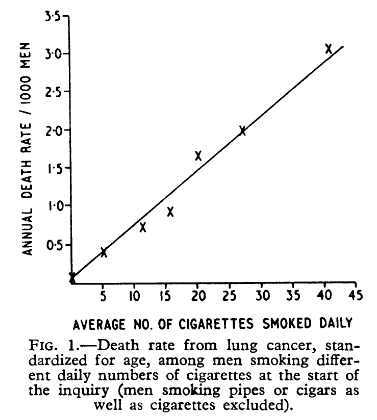
The British Doctors Study, which began in 1951, was the world’s first large prospective study of the effects of smoking to establish a convincing linkage between tobacco smoking and cause-specific mortality, and demonstrated prospectively the risk of death from lung cancer (1954) and myocardial infarction and chronic obstructive pulmonary disease (1956).

In October 1951, Sir Richard Doll and Sir Austin Bradford Hill sent a questionnaire on smoking habits to all registered British doctors. Of the 59600 questionnaires mailed, 41024 replies were received and 40701 (34494 males and 6207 females) were sufficiently complete to be included in the follow-up. Because of the limited sample size and limited tobacco consumption females were excluded from most reports, and the study has focused on the males. Source

  • Is this a representative sample of the population of

    • British doctors?
    • British men who are well educated?
    • British men?
    • Men of all nations?
    • All people?

Representative Samples

1954

Chart showing variation in mortality with amount smoked. R. Doll and A. B. Hill, “The Mortality of Doctors in Relation to Their Smoking Habits; a Preliminary Report,” British Medical Journal 1, no. 4877 (June 26, 1954): 1451–55, https://doi.org/10.1136/bmj.1.4877.1451.

Chart showing variation in mortality with amount smoked. Doll and Hill.

1964

Chart showing variation in mortality with amount smoked daily. Richard Doll and Austin Bradford Hill, “Mortality in Relation to Smoking: Ten Years’ Observations of British Doctors,” Br Med J 1, no. 5395 (May 30, 1964): 1399–1410, https://doi.org/10.1136/bmj.1.5395.1399.

Representative Samples

Scientific generalization vs. Statistical generalization

  • Science goal: Make correct statements about the way nature works

  • Statistics goal: Extrapolate from a sample to the source population

These goals may align, but they may not!

Whether a sample is representative enough to generalize beyond the sample population is determined by your argument.

Representative Samples

\[\left(\begin{array}{c}\text{limiting confounding variables}\\ \text{non-representative population}\end{array}\right) \overset{?}{\geq}\left(\begin{array}{c} \text{no control over confounds}\\\text{representative population}\end{array}\right)\]

The best case for generalizing results is if there are

  • consensus findings

  • from studies using different designs

  • across different populations

  • by different research groups.

Interaction Interpretation

Misconception: Lack of statistical interaction => lack of real-world interaction

  • Statistical interaction effects are conditional on the specific model and data

  • Model lack of fit => interaction may not be significant even if real-world effect exists

  • Data collected over wrong range?

All models are wrong, but some are useful – George Box

Significance Testing

‘Detector! What would the Bayesian statistician say if I asked him whether the–’ [roll] ‘I AM A NEUTRINO DETECTOR, NOT A LABYRINTH GUARD. SERIOUSLY, DID YOUR BRAIN FALL OUT?’ [roll] ‘… yes.’

The null is MUCH MORE LIKELY than the alternative!

Significance Testing

  • Null Hypothesis Significance Testing (NHST) is a combination of two distinct testing philosophies (More Reading)

  • It is often more important is to understand the size of the effect

  • Confidence intervals provide both effect size and precision!

    • (and don’t have to be reduced to is the null value in here?)

Assess both statistical significance and practical significance when assessing and interpreting results

Manager Misconceptions

Manager Misconception Examples

  • Just rerun the experiment with a bigger sample size!

  • Statisticians can predict exactly what will happen next 🔮🪄🧙

A gif of a man being swatted on the nose with a newspaper by a dog, with the text 'No, Bad!' at the bottom.

Address these issues in person if at all possible. Try not to laugh or cry.

References

Doll, R., and A. B. Hill. “The Mortality of Doctors in Relation to Their Smoking Habits; a Preliminary Report.” British Medical Journal 1, no. 4877 (June 26, 1954): 1451–55. https://doi.org/10.1136/bmj.1.4877.1451.
Doll, Richard, and Austin Bradford Hill. “Mortality in Relation to Smoking: Ten Years’ Observations of British Doctors.” Br Med J 1, no. 5395 (May 30, 1964): 1399–1410. https://doi.org/10.1136/bmj.1.5395.1399.
Gershman, Samuel J., and Tomer D. Ullman. “Causal Implicatures from Correlational Statements.” PLOS ONE 18, no. 5 (May 18, 2023): e0286067. https://doi.org/10.1371/journal.pone.0286067.
Motulsky, Harvey J. “Common Misconceptions about Data Analysis and Statistics.” Naunyn-Schmiedeberg’s Archives of Pharmacology 387, no. 11 (2014): 1017–23. https://doi.org/10.1007/s00210-014-1037-6.
Rothman, Kenneth J. “Six Persistent Research Misconceptions.” Journal of General Internal Medicine 29, no. 7 (January 23, 2014): 1060–64. https://doi.org/10.1007/s11606-013-2755-z.