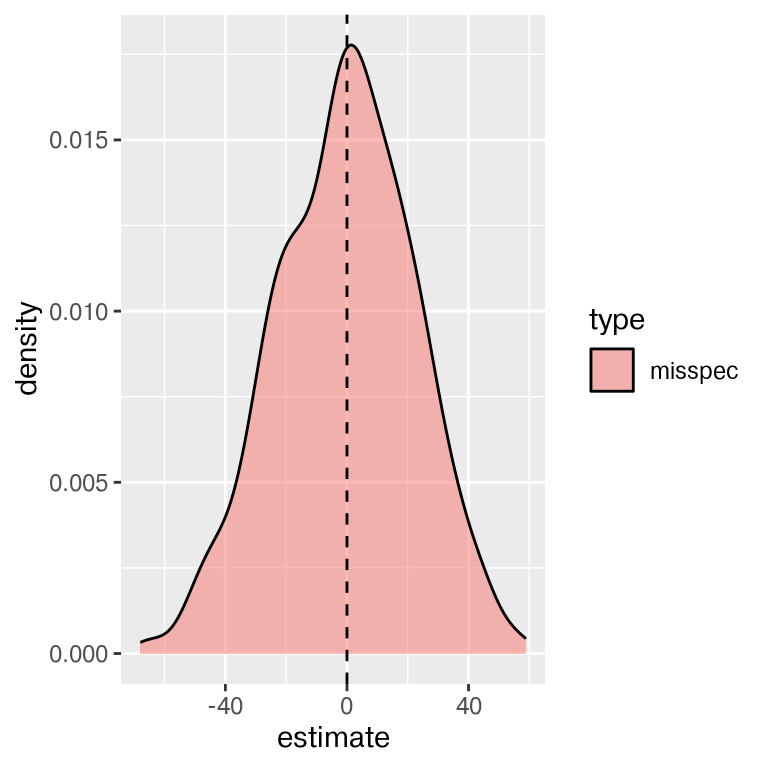
Call:
lm(formula = y ~ x1 + I(x1^2), data = data)
Residuals:
Min 1Q Median 3Q Max
-29.1382 -6.9539 -0.2898 5.4694 30.6999
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.30483 1.55887 -0.837 0.405
x1 0.90094 0.17844 5.049 2.08e-06 ***
I(x1^2) 0.51842 0.03407 15.214 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 10.41 on 97 degrees of freedom
Multiple R-squared: 0.7261, Adjusted R-squared: 0.7205
F-statistic: 128.6 on 2 and 97 DF, p-value: < 2.2e-16Simulation Using Built-In Functions
Linear Regression Assumptions
Linearity and Additivity of DVs
Independence of Errors
Constant Variance of Errors
Normality of Errors
How Bad is it? – Linearity
library(tidyverse)
set.seed(2034927344)
data <- tibble(
x1 = seq(-10, 10,
length.out = 100) +
runif(100, -.1, .1), # wiggle
x2 = seq(10, -10,
length.out = 100) +
runif(100, -.1, .1), # wiggle
# Definitely not linear
y = x1 + x1^2/2 + # main effect
rnorm(100, 0, 10) # actual error
)
ggplot(data, aes(x = x1, y = y)) +
geom_point()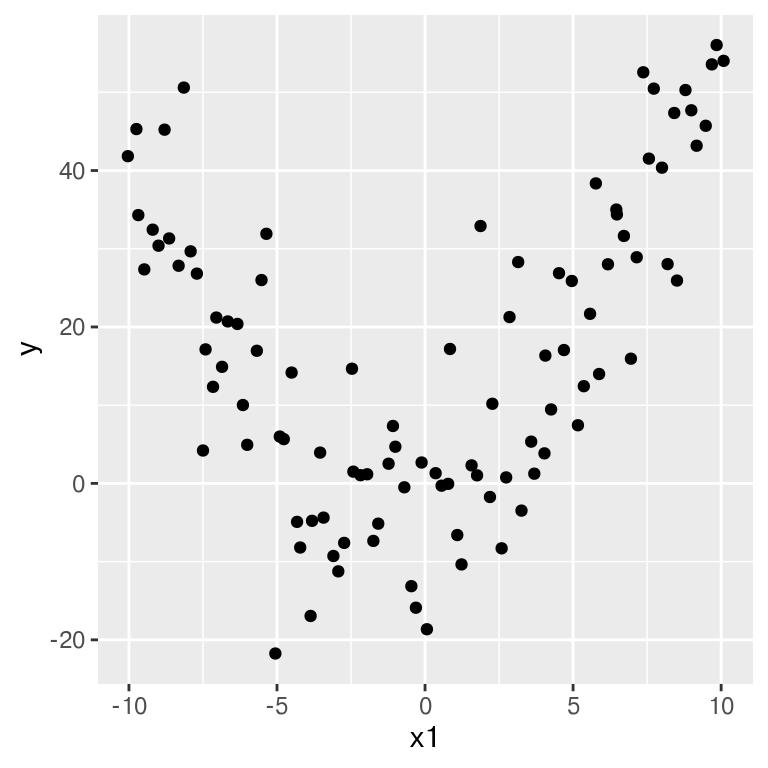
Clearly non-linear
How Bad is it? – Linearity
Call:
lm(formula = y ~ x1 + x2, data = data)
Residuals:
Min 1Q Median 3Q Max
-35.805 -15.641 -1.853 16.714 44.165
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 16.457 1.913 8.605 1.37e-13 ***
x1 -20.473 24.200 -0.846 0.400
x2 -21.413 24.238 -0.883 0.379
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 19.08 on 97 degrees of freedom
Multiple R-squared: 0.07991, Adjusted R-squared: 0.06094
F-statistic: 4.212 on 2 and 97 DF, p-value: 0.01761How Bad is it?
Models
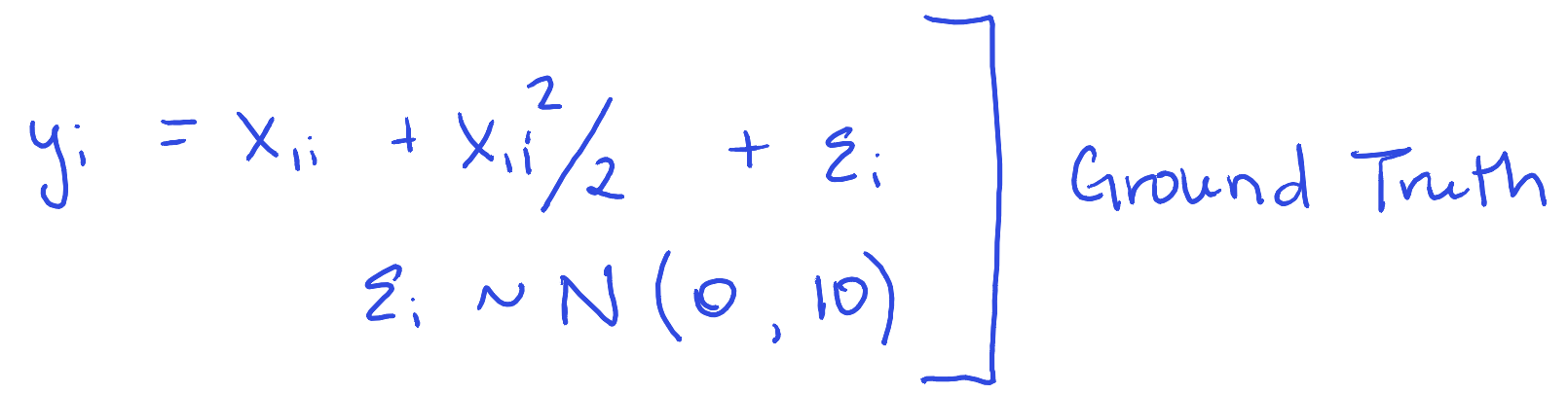
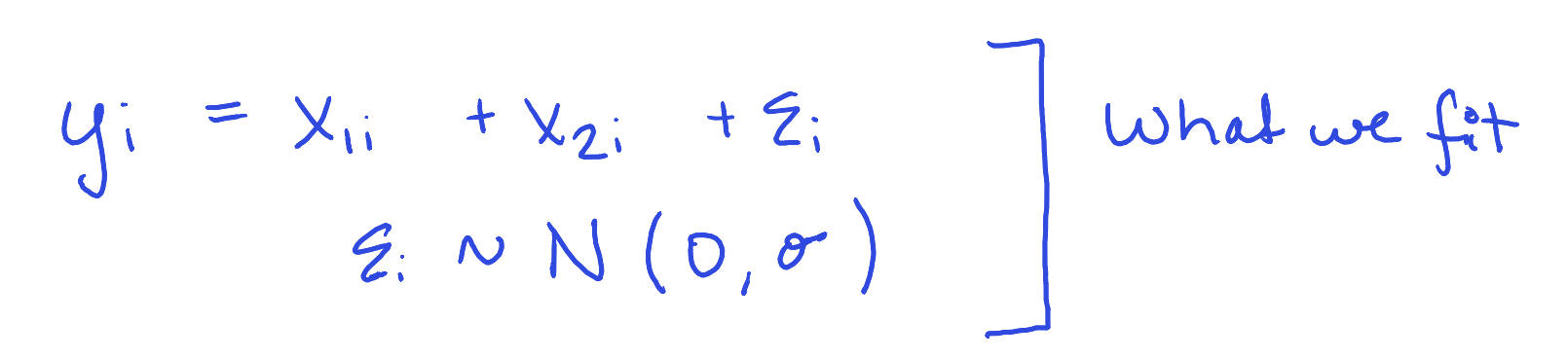
Simulation – Questions
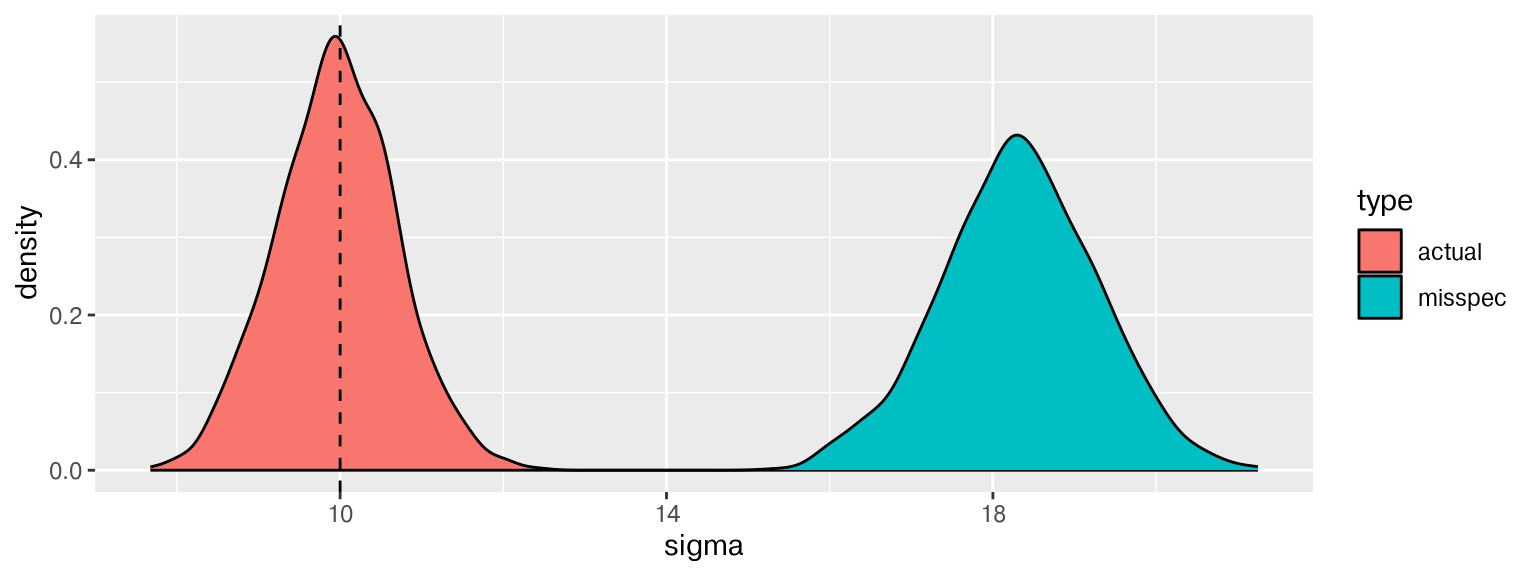
- How does \(\hat{s}\) compare to \(\sigma=10\)?
- How does \(\hat\alpha\) compare to true value \(\alpha=1\)?
- How does \(\hat\beta\) compare to true value \(\beta=0\)?
Simulation – Linearity assumption
sim_linearity <- function(i, n = 100, formula = y ~ x1+x2, trueformula = y ~ x1 + I(x1^2)) {
data <- tibble(
x1 = seq(-10, 10, length.out = n) + runif(n, -.1, .1),
x2 = seq(-10, 10, length.out = n) + runif(n, -.1, .1),
y = x1 + x1^2/2 + rnorm(n, 0, 10) # Definitely not additive or linear
)
model <- lm(formula = formula, data = data)
model2 <- lm(formula = trueformula, data = data)
tibble(
i = i,
data = list(data),
model = tibble(type = c("misspec", "actual"),
model = list(model, model2))
)
}
set.seed(249382736)
sim_n <- map_df(1:1000, ~sim_linearity(.)) |>
unnest(model)Simulation – Getting Estimates Out
Error Variance
\(\alpha\) coefficient
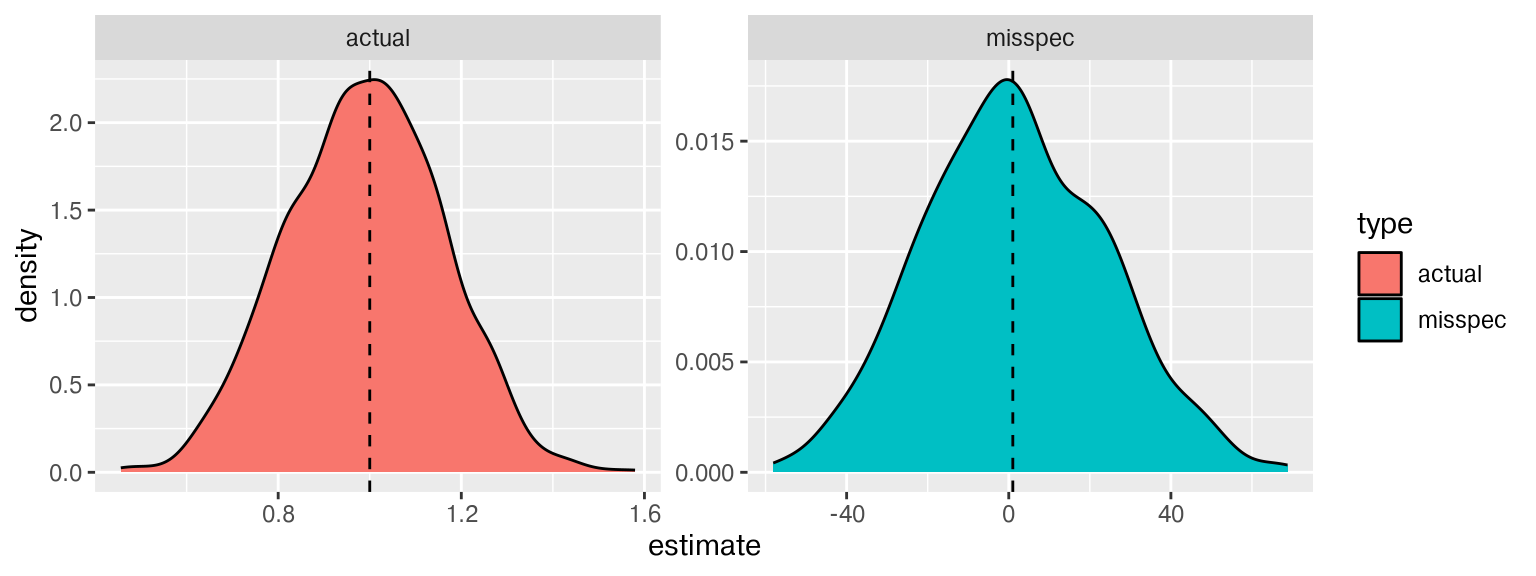
That is some wide error variance!